Professor Howard Colquhoun tells the story of how an infinitely repeating pattern discovered in a plastic molecule relates to obscure 19th century maths – and Romanesco broccoli.

In 1874, Henry J. S. Smith, Professor of Geometry in the University of Oxford, had an interesting thought. “What would happen,” he wondered, “if you took a line, divided it into four, and then threw away the end quarter?”
Well, obviously, you would be left with a line three-quarters as long as the original.
But Smith’s next question was more subtle. “What would happen if you repeated this operation on the line that was left, and then continued to do this indefinitely?”
When Smith worked through the problem, it turned out that he had discovered the first ever example of a fractal, a mathematical structure that is made up of an infinite number of progressively smaller copies of itself.
A few years later, the German mathematician Georg Cantor discovered a number of closely-related examples and, despite Smith’s prior discovery which was published in 1875 in the Proceedings of the London Mathematical Society, such fractals are now universally known as Cantor Sets.
The best-known ‘real’ object that shows fractal geometry is probably Romanesco Broccoli (below), a vegetable that has a spiral structure made up of many smaller spirals, which are themselves made up of smaller spirals still, and so on.
And the best known ‘mathematical’ fractal is certainly the Mandelbrot set, which, on magnification reveals a vast wealth of remarkably beautiful detail.
The Mandelbrot set (top image), and the detail within it (lower image).
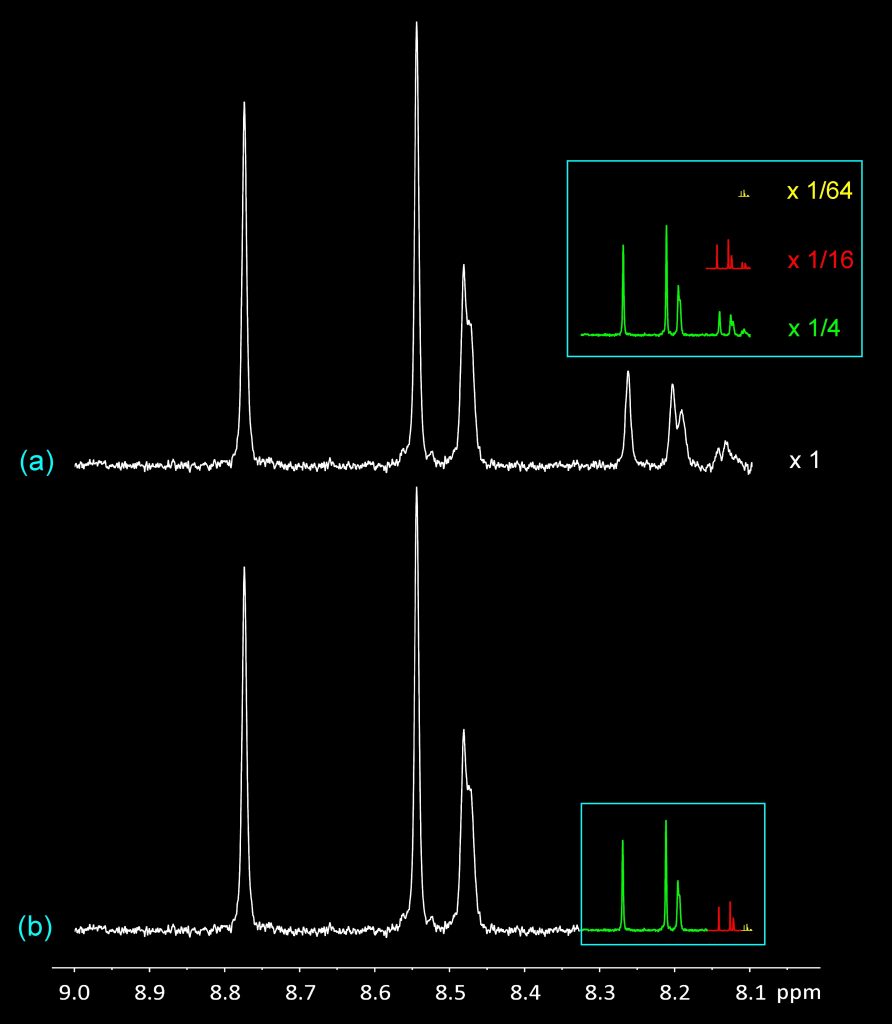
The fractal that Smith had discovered remained just a rather obscure mathematical construct for well over a hundred years. Then in 2010, a PhD student, John Shaw, working with me at the University of Reading, discovered a very unusual pattern in the nuclear magnetic resonance (NMR) spectrum of a polymer he was analysing.
The pattern seemed, astonishingly, to be made up of several smaller copies of itself (does this start to sound familiar….?). Subsequent work by other researchers in the Department of Chemistry confirmed John’s result and enabled the construction of a detailed atomic model for the polymer system that had produced the fractal-like spectrum.
An analysis of the data by Dr Ricardo Grau-Crespo, Lecturer in Chemistry at Reading, then revealed that the model leads directly to an equation that is the definition of Smith’s original fractal, now called the ‘Fourth-Quarter Cantor Set’.
Even more intriguingly, this equation accurately predicts the spectrum discovered by John Shaw. So that an apparently obscure result in 19th Century mathematics has now emerged as a complete description of some new and fascinating real-world polymer chemistry.
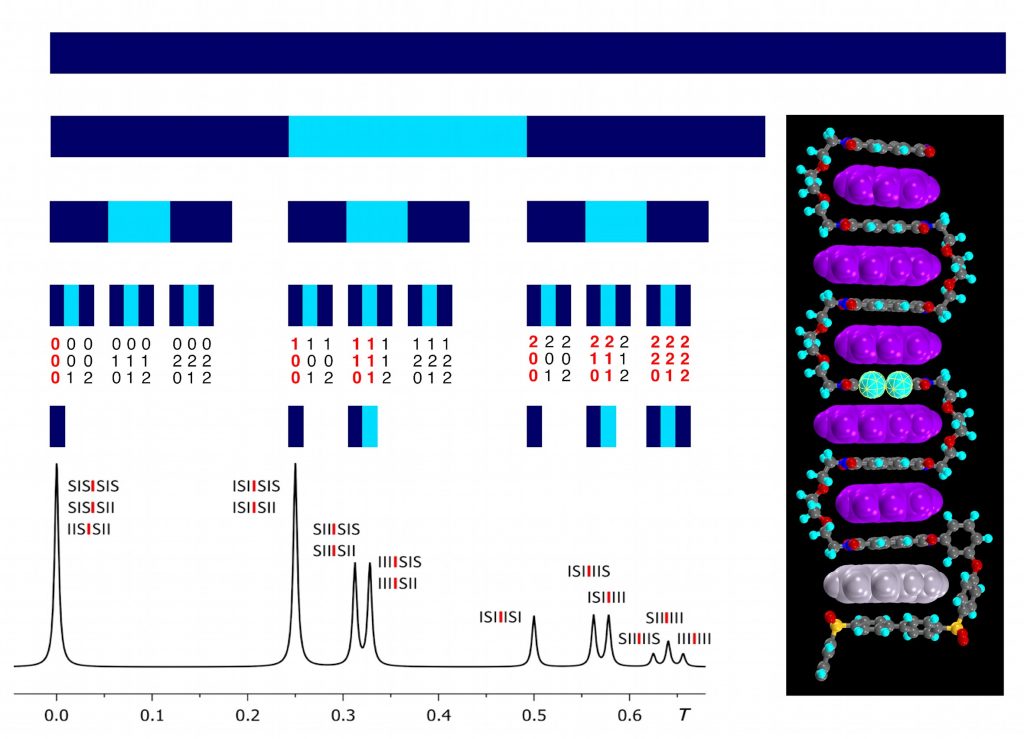
Construction of the fourth-quarter Cantor set and its prediction of the NMR spectrum of the polymer-complex shown at right.
Experimental NMR spectrum of the polymer-complex showing how it consists of several smaller copies of itself.
Going back to Henry Smith’s original idea, the images shown above illustrate the construction of his fractal and show how the construction predicts the NMR spectrum observed at Reading. The work has just been accepted for publication by the Royal Society of Chemistry, in their flagship journal Chemical Science.
Read today’s press release about this paper and the future potential of fractal patterns in molecules as a way of efficiently storing information. Howard Colquhoun is Professor of Materials Chemistry at the University of Reading.