How do scientists understand highly complex and intricate systems such as the atomic structure of materials, stars in a remote region of our galaxy, or even our planet Earth itself?
They just kick them and observe the reaction.
It might sound very naive at first glance, but this approach actually stems from a solid and well developed mathematical framework, called Linear Response Theory.

The main goal of the theory is to investigate the connection between the observed response and the system before the perturbation. It turns out that, by analysing how it reacts, we get a great insight into the properties of the system itself.
Common sense suggests that “to a small cause corresponds a small effect”. After a tiny perturbation, the response is going to be small and will eventually fade away. Everyday life seems to support this saying. I guess you have never heard of anyone dropping their morning cup of coffee and consequently breaking their whole house into pieces. Hitting the floor, the cup will probably shatter, spilling coffee all over the place. The perturbation is not small for the cup – but the house is very likely to remain intact.
Nature and society, on the other hand, do not seem to conform to this saying. Forests can suddenly turn into savanna, financial markets crash, ecosystems collapse for no apparent triggering reasons. These are just a few examples of a huge variety of phenomena, commonly known as critical transitions, that happen more often than you might think.
Critical transitions are characterised by an abrupt, sudden, substantial – and usually unpleasant – change of the system.
Close to a critical transition, common sense fails. A small perturbation can kick the system very far away from its original state, leading to catastrophic unforeseen consequences. A ’critical’ house could literally collapse as soon as the cup hit the floor.
Much effort has been put into developing mathematical techniques to assess whether a system is close to a critical transition. Successfully doing so might allow action to be taken before that critical ‘tipping point’ was reached, or taking care to avoid the critical jolt that causes a large change, such as to Earth’s climate.
These techniques are fairly general and seem to perform quite well in a huge variety of situations observed in different areas of nature, from biological to social sciences. They are not infallible though.
In our work we identified an important class of systems exhibiting critical transitions that are able to elude these techniques.
In a recent study carried out at the University of Reading, we examined a generic system composed of many interacting subsystems. As the number of subsystems increases, its structure gets more and more complex, see Fig 1.
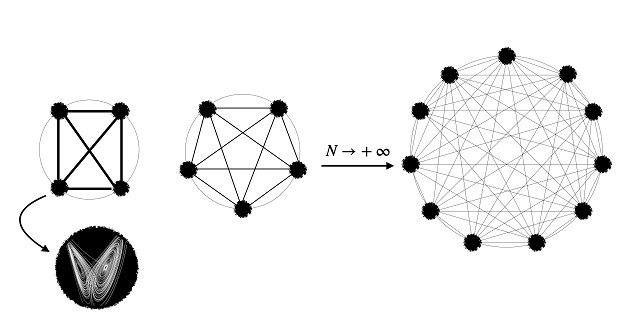
When the system is sufficiently complex, critical transitions may arise. This (very general) mathematical framework is able to explain rather interesting critical transitions that are often observed in Nature, namely order-disorder and synchronisation transitions.
If this sounds very abstract and remote, worry not!
Have you ever wandered in the countryside on a chilly spring night away from the lights of the city? If you were lucky, you probably saw some fireflies flying around. If you were even luckier, you might have witnessed the magical moment in which some species of fireflies synchronise and emit light in an organised manner.
Think of the fireflies as the subsystems, and of the light they emit as the coupling between them, and you will soon realise that fireflies represent exactly the system we are investigating.
But how can we predict the onset of synchronisation in fireflies if the usual indicators fail? We kick them! (Not literally of course)
Linear response theory is the answer. If you were able to convince a relevant (but still small) subset of fireflies to emit light at the same time, you would see that in critical situations the whole system would respond accordingly and synchronise. In non-critical situations, the initial kick would soon be forgotten and nothing would happen.
Unfortunately, other types of critical transitions are not as nice. Epileptic seizures are an example of a negative effect of synchronisation of neurons firing at the same time.
However, the mathematical framework we developed can still be applied.
Ideally we would like to develop a new set of tools that allow us to forecast the onset of this new type of critical transitions solely based on the data we have about the system.
Our work on this continues.
Niccolo Zagli is a former PhD student in the Department of Mathematics and Statistics.
