By Eviatar Bach
My name is Eviatar Bach, and I recently started as a Lecturer in Mathematics of Environmental Data Science at Reading. I have a joint appointment between the Department of Meteorology and the Department of Mathematics and Statistics. Besides DARC, I am also part of the Centre for Mathematics of Planet Earth, and an Outreach Officer for the Centre for Doctoral Training on Mathematics for Our Future Climate.
I am very excited to join Reading and to collaborate with the excellent researchers here, as well as to start my own research group!
A little bit about my academic background: I obtained my bachelor’s degree in 2017 at the University of British Columbia in physics and computer science, with a minor in mathematics. I then attended the University of Maryland, College Park, receiving my PhD in Atmospheric and Oceanic Science in 2021, advised by Eugenia Kalnay (who very sadly passed away in August of this year; here is a nice obituary about her) and Safa Mote. I then moved to École Normale Supérieure in Paris as a postdoctoral fellow working with Michael Ghil. As a second postdoc, I moved to the California Institute of Technology, where I was a postdoctoral fellow working with Tapio Schneider and Andrew Stuart.
My research interests are quite broad. I provide a brief overview of my past research related to data assimilation and predictability below. I am also interested in (and have worked on) other aspects of climate, inverse problems, and nonlinear dynamics, but that is perhaps for a future post.
I am currently looking for PhD students and always open to new collaborations, so please do not hesitate to contact me if you’re interested. See also my personal website for more information.
Data assimilation
Data assimilation (DA) is, as readers of this blog may know, the process of combining observations and model forecasts. I work primarily on ensemble DA, which expresses uncertainty through forecasts started with different initial conditions.
In the past few years, I have been working on the integration of machine learning and data assimilation in several directions.
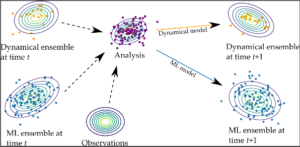
One direction is the use of machine learning forecast models in DA. One approach is to use just the machine learning model for forecasts, as we did in Chattopadhyay et al. (2022). Machine learning forecast models can also be used in DA in a hybrid way along with dynamical models; see Chattopadhyay et al. (2023). I have worked on a multi-model ensemble Kalman filter (Bach and Ghil, 2023) that provides a principled hybrid approach, and also on combining dynamical models with data-driven forecasts of predictable modes (Bach et al., 2021).
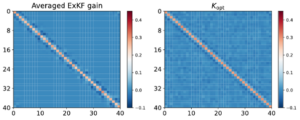
More recently, I have become interested in the problem of machine learning of DA algorithms. In Luk et al. (2024), we approached this with variational inference, a method for solving Bayesian inference problems using optimisation. We are actively pursuing this direction further.
Recently, Ricardo Baptista, Daniel Sanz-Alonso, Andrew Stuart, and I put together a collection of lecture notes on machine learning in data assimilation and inverse problems.
Forecasting and predictability of climate and weather
The limits on predictability of midlatitude synoptic-scale weather have long been known. However, it is also known that there are sources of predictability beyond this limit, especially in the tropics and when looking at time-averaged quantities. The subseasonal-to-seasonal timescale, two weeks to several months, is especially promising in this regard. Sources of predictability include slowly evolving sea-surface temperature and soil moisture, intraseasonal oscillations, and interactions with the stratosphere.
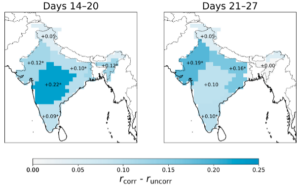
However, dynamical models generally have poor skill at subseasonal-to-seasonal timescales due to accumulated biases. Machine learning presents an opportunity here. In Bach et al. (2024a), we showed that data-driven forecasts of monsoon intraseasonal oscillations can be combined with dynamical ensembles to significantly improve South Asian monsoon forecasts, based on the methodology of Bach et al. (2021). I am currently pursuing this direction further using the more advanced method of Bach and Ghil (2023).
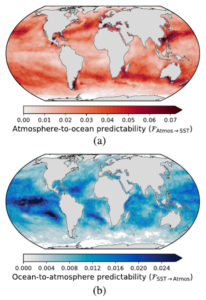
In Bach et al. (2019), we examined from data the predictability that the ocean provides to the atmosphere, and vice versa. In Penny et al. (2019), we examined the predictability of an atmosphere-ocean model in coupled and uncoupled configurations through its Lyapunov spectrum. In Bach et al. (2024b) we propose a simple stochastic model for forecast error growth of numerical weather prediction.
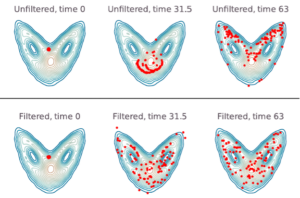
In Bach et al. (2024c), we devised a method to assimilate information about a system’s statistical properties rather than state observations, and demonstrated that this can be used to spin up models more quickly to equilibrium. We are also testing this method for correcting model errors.

