by Tom Block
A quick view on history
The idea of the Earth not being flat is a very old one. Early Mesopotamian mythology visualized the Earth as a flat disk, floating on the ocean and surrounded by a spherical sky. However, already in the 3rd century BC Hellenistic astronomers established the spherical shape of the Earth as physically given.
Interestingly, this early breakthrough insight is mostly being ignored by modern geographic software libraries, database implementations and other GIS systems. We will check why this happens, what the benefits and the drawbacks are and why this is relevant for FIDUCEO. And – finally – present a different, very elegant solution.
Why do we care about this?
When searching for matchup-data, i.e. coinciding measurements of the same location on Earth at almost the same time using different space borne instruments, we need to detect geographically overlapping areas of different satellite sensors. We do this by calculating a polygon matching the bounding area of each satellite acquisition and then calculate the geometrical intersections of a large number of these polygons. When a not-empty intersection is detected and the timing information matches the constraints, we have detected an area where matchups may possibly be found.
These matchup-datasets are an integral input for the harmonisation of long sensor time-series (please check the blog of Emma Wooliams for details on this).
In FIDUCEO we generally operate with L1 satellite acquisitions which in most cases span the complete planet for each “orbit-file”. As we have a lot of them (the latest census results in >1.7 Million input files) the selection of a software library for geometric operations is crucial, both in terms of precision and performance.
Planar Coordinates
Any planar coordinate system tries to map the Earth ellipsoid onto a two-dimensional map. There exist a large number of projections which minimise different effects of the distortion inevitably introduced (e.g. area-, shape-, distance-, whatever-distortion). Common to all of these are the rather complex transformation equations that often make use of trigonometric functions – which slow processing down significantly.
The easiest projection used in modern geo-information systems is the plate-carrée projection with the very simple transformation equations:
x = \lambda
y = \phi
It has some nice features that establish its popularity: the transformation equation is extremely simple and geographic coordinates can directly be read from the map.
Common to all map projections is the map, which by definition is flat and limited in extension; it has a left and a right border, also the top and the bottom of the map are limited. Everything evil happens at these borders, see Figure 1!

Figure 1: : AVHRR NOAA 8 acquisition in plate-carree projection.
When applying any map projection to an Earth-spanning satellite acquisition, the originally smooth and continuous acquisition data geometry is distorted and split into pieces by the map projection. Every border of the map, when crossed by the acquisition data, generates new segments of the geometry, and distortion increases when approximating to the poles (or other singularities of the projection).
This behaviour can be ignored when operating only on small data granules away from the poles and most geometry libraries like JTS or GeoTools seamlessly work in these regions – but they fail miserably when using full-orbit geometries.
Long segments of additional code are required to pre-process satellite orbit geometries for use with two-dimensional geo-libraries: splitting at anti-meridian and longitude-shifting the segments, detecting poles in the polygon (difficult) and compensating for that (even more difficult). This makes the software slower and more complex than it should be.
Spherical Coordinates
Spherical coordinate systems on the other hand are also basically a lie when it comes to the planet, as its form is a flattened ellipsoid. But ignoring this fact allows us to use rather simple mathematic formulae to overcome most of the problems listed above without sacrificing too much of the precision. Notabene: when working with the satellite data we use in FIDUCEO, we do not really care about one or two meters.

Spherical coordinate systems are inherently cyclic. This way we can avoid all the problems encountered with planar coordinates when it comes to the borders of the coordinate system – because these do not exist. The anti-meridian and the poles nicely integrate; no extra code is required to handle these. The only problem still remaining is the acquisition self-overlap – which can easily be handled by splitting the acquisition in two parts (see Figure 2).
Figure 2: The same AVHRR NOAA 8 acquisition in a spherical coordinate system – with a self-overlapping area.
Still there exists the problem of performance because calculations using spherical polygons heavily involve trigonometric function. This might be negligible for a single calculation and in the range of milliseconds when not executed on special-purpose hardware – but 1 Million milliseconds are ~17 minutes – and we want to be processing fast and avoid this.
A significant Speed-Up
Now we’d like to introduce a true treasure that overcomes all the problems mentioned: The Google S2 library. This is a geometric library published by Google which operates on a sphere but introduces some very interesting concepts to combine precision and performance with mathematical beauty. We give just a short overview of the concepts and suggest that the more interested reader follows the embedded reference links
In a first step, the unit-sphere is projected onto the unit-cube, thus performing some kind of map-projection, but inherently keeping the three-dimensional aspects of a spherical coordinate system. So, addressable locations on the surface of a sphere are transformed to locations on the surfaces of a cube (see Figure 3). The distortion in distance caused by the projection needs to be compensated for, which is cleverly done by replacing the inevitably occurring trigonometric arctan function by a quadratic approximation.
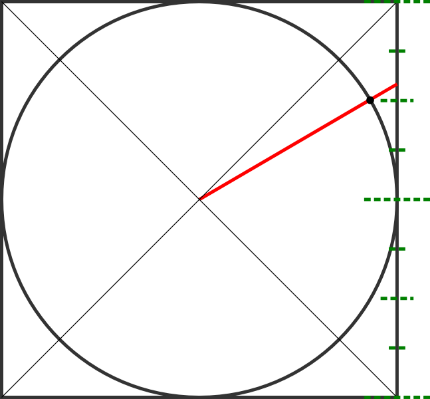
Figure 3: Projection of the sphere onto the unit-cube. From “Geometry on the Sphere: Google’s S2 Library” by Octavian Procopiuc
Addressing of locations on each of the surfaces of the cube is realised using the run-length along a Hilbert curve which fills each of the faces of the cube – because it is a space filling fractal curve. This has to two benefits: an inherently three dimensional addressing problem is mapped onto two entities, the index of the face and the length along the Hilbert curve. Secondly, neighbouring properties in the 2D-coordinate space of a surface are kept, i.e. points close to each other on the surface are also close to each other on the length of the Hilbert curve (see Figure 4).

Figure 4: Addressing the cells on a face of a unit-cube using a Hilbert-curve. From “Google’s S2, geometry on the sphere, cells and Hilbert curve” by Christian S. Perone
The index of the face and the length along the curve are finally merged into one integer number, so that a longitude/latitude floating point coordinate of the sphere is mapped onto a single integer value.
These concepts have been used by software developers at Google to build a geometric library, implementing the known entities like “POINT”, “LINESTRING, “POLYGON” etc. and the most common operations on these objects, like “intersects”, “contains”, etc. .
Unfortunately, there is not much documentation provided with the library, there exists a set of slides explaining the basic concepts and a blog by Christian Perone discussing the concepts and showing some examples. The core library is written in C, there exists a partial port of the code to Java.
After some initial tests, we were so convinced by the library that we extended the original Java library to our needs and happily integrated it into the FIDUCEO processing code.
Conclusion
The Google S2 library is an important building block in our software development toolset when using geometric operations, geometric indexing or a combination of both. It comes with automated unit-level tests and has proven to be extremely reliable during the last years. We literally processed hundreds of Terabytes of data with it.
Beyond FIDUCEO, we at Brockmann Consult use the library as a core component for the geographic index of our Calvalus processing cluster.
The updated version of the library is GPL licensed and available at: https://github.com/FIDUCEO/MMS/tree/master/google-s2
The updates consist of some methods being ported from the C-version of the library to Java and the implementation of some utility methods and conversion facilities to and from the WKT representation of geometric objects.